Kaderi Baştan Yazılmış Olan Bilgisayarlar Nasıl Rastgele Sayı Üretebiliyor?

Rastgele sayıları kullanmadığımız yer var mı? Çekilişler, oyunlar, dosya isimleri, simülasyonlar, parola oluşturucular, istatistik, sanat… Bu liste uzar gider. Yalnızca sayılar değil, rastgele sayılardan türetilmiş farklı veri türleri de bu işlerin bir kısmında kullanılabilir. Yalnız şöyle bir durum var; tüm bunları bilgisayar üzerinde yapabiliyoruz, ancak bilgisayarın kendisi yapısı gereği gerçek anlamda rastgele sayı üretememekte.

Bilgisayar açıldığı andan itibaren dışarıdan bir veri alana kadar gerçekleşecek her şey bellidir. Dışarıdan bir veri geldiğinde, örneğin bir mouse hareketi gerçekleştiğinde bunu da kullanıcı kendi bilinci dahilinde gerçekleştirdiği için rastgele olarak görmeyiz. Tabii böyle bir girdiyi sayısal olarak yorumlayarak anlık olarak rastgele bir değer olarak yorumlamak da bir fikir. Bunu yapan uygulamalar da yok değil, Windows üzerinden dışarıya SSH bağlantısı kurmayı sağlayan PuTTY buna bir örnek.

Söylediğim gibi, bilgisayarda her şey kesindir. Bilgisayar, üzerine programlanmadığı bir şey düşünemez, rastgele bir veri üretemez. Onun kaderi ya baştan bellidir, ya da verilen girdilerle şekillenecektir. O yalnızca elektrik akımlarından oluşmuş “zihniyle” dışarıdan aldığı veya halihazırda üzerinde bulunan veriler üzerinden işlem yaparak bir çıktı üretir. Bize de bu çıktıyı sunar. Söz konusu rastgele sayı beklentisi olduğunda ise bizi şaşırtacak veya beklemediğimiz bir sonuç gerekiyor.

Bunu çeşitli yöntemlerle gerçekleştirebiliyoruz. Bunlardan en bilineni, en sık kullanılanı ve en basiti Sözde Sayısal Rastgele Sayı Üreteci (Pseudorandom Number Generator - PRNG) adını verdiğimiz bir kategori. Aritmetiği kullanarak, sayıları işleyerek ve bir kısmını da duruma göre yok ederek beklemediğimiz sayılarla karşılaşıyoruz. Elbette bu yöntemin birçok sıkıntısı var, bunlara daha sonra değineceğim.

PRNG yöntemlerine Orta Kare Metodu (Middle-square Method) ile başlayalım. Bu yöntemi anlaması çok basit. Öncelikle tüm PRNG yöntemlerinde kullanacağımız tohum (seed) kavramına bir bakalım. Yalnızca yüksek seviye programlama dilleriyle uğraşmamışsanız bu seed kavramına aşina olmanız beklenebilir. Seed bizim çıkış noktamız, rastgele sayıların üretileceği zincirin alması gereken ilk değer. Bu genellikle sistemin o anki saati olarak belirlenir. Biz ise şimdilik elle belirleyelim. Orta Kare Metodu için öncelikle bize n basamaklı bir sayı gerekiyor, bu bizim için 6 basamaklı “675248” olsun. Bu sayının karesini alıyoruz ve “455959861504” şeklindeki 2n, yani 12 basamaklı sayıya ulaşıyoruz. Bazı durumlarda 2n basamaklı değil, eksik sayıda basamak çıkabilir. Bu durumda sol kısma 0 ekleyerek 2n’e tamamlıyoruz. Şimdi ise yapacağımız şey tam ortasındaki n basamaklı sayıyı almak. 959861 bizim sözde rastgele sayımız. Tekrar bir rastgele sayı üretmemiz gerektiğinde ise 959861 sayısının karesini alacağız, o da bize 921333139321 sayısını verecek, oradan da 333139 sayısına erişeceğiz ve bu böyle gidecek. Elimizde beklenmedik bir sayı var ve önceki sayıyı tahmin etmemiz zor, çünkü veri çıkardık. Bu yöntem oldukça ilkel olsa da bir gün rastgele sayı üreteci yazmanız gerektiğinde hızlıca yazabileceğiniz bir algoritmaya sahip. Yalnız çok önemli problemleri olduğunu söylemek gerek. Örneğin diyelim bu işlemi 4 basamaklı sayılarla yapıyorsunuz. 2500’e ulaştığınızda ağlayarak günlüğünüze yazabilirsiniz. Çünkü 2500’in karesi 6250000 ve bunun ortasındaki 4 haneli sayı yine 2500. Burada bir kısır döngüye giriyorsunuz ve yapı artık rastgele sayı üretememeye başlıyor.

Şimdi bahsedeceğim PRNG yöntemi ise Doğrusal Uyumlu Üreteç olarak çevirebileceğimiz Linear Congruential Generator. İsmine aldanmayın, çok uyduruk bir yöntem. Tabii uygun parametreler seçildiğinde tatmin edici düzeyde başarılı olduğunu da söylemek lazım. Bu yöntemi GNU/Linux’ta C kodu derlediğinizde kullanıyorsunuz aslında. glibc, dolayısıyla da GCC bunu kullanıyor. Yöntem çok basit. Bir adet seed yine gerekiyor, bir adet mod, bir adet çarpan, bir de ek gerekiyor. Moddan kastımı anlamışsınızdır, bölümünden kalanı alacağımız bir sayı. Yapacağımız şey ise şu: sonuç = (çarpan * seed + ek) % mod Çıkan sonucu ise bir sonraki rastgele sayının seed’i olarak kullanacağız ve bu, bu şekilde gidecek. %’nin modulus işlemi olduğundan bahsetmeme gerek yoktur herhalde. LCG isimli bu yöntem aşina olduğumuz birçok platformda kullanıldı ve kullanılıyor. Java, Turbo Pascal, Visual Basic, Borland Delphi, Borland C/C++, ANSI C ve bahsettiğim gibi GCC. Daha da uzuyor gidiyor. Örneğin ANSI C ve GCC’nin varsayılan değerlerini inceleyelim: mod: 2^31 çarpan: 1103515245 ek: 12345 Bu metotlar yeterince rastgele görünen sayılar üretebilmek için çoğunlukla yeterli oluyor.

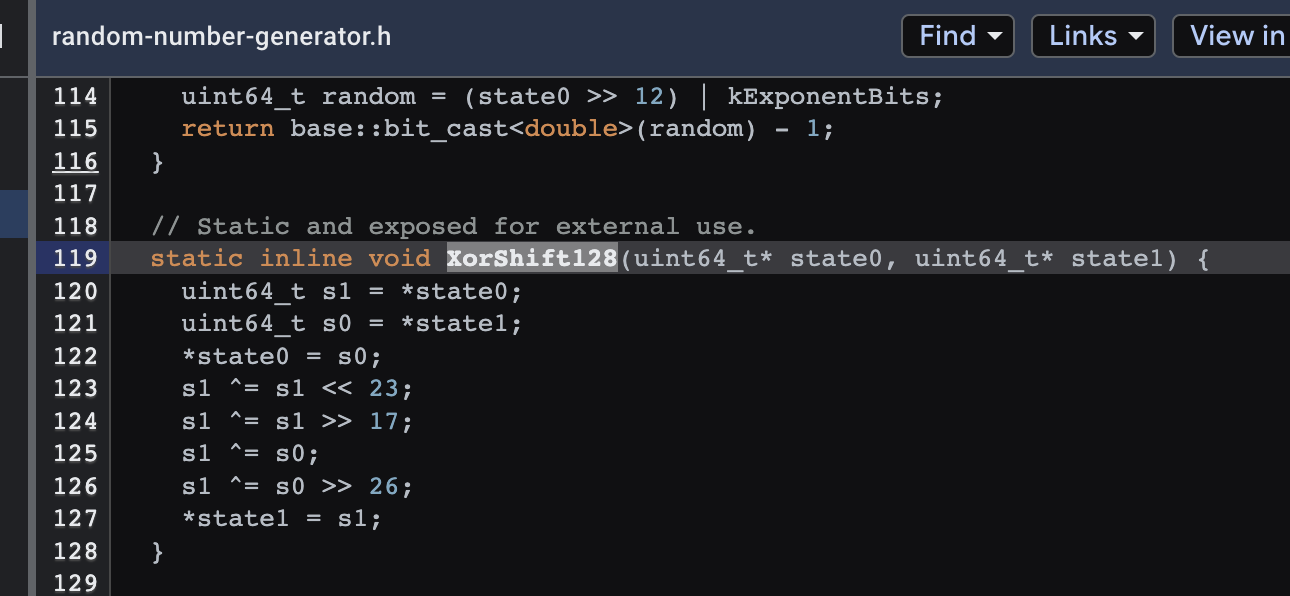
Bu aritmetik yöntemlerden son olarak V8 motorunun, dolayısıyla da günümüzde JavaScript çalıştıran çoğu ortamın kullandığı yöntemden; XorShift128+ algoritmasından bahsedelim. Bu algoritmada da verilen seed değeri önce bit düzeyinde 23 kere sola kaydırılıyor ve çıkan değer kendisiyle Xor’lanıyor, ardından bunun sonucu 17 kere sola kaydırılıyor ve kendisiyle Xor’lanıyor, bunun sonucu da ilk adımdaki haliyle Xor’lanıyor derken son olarak da ilk adımdaki değer 26 kere sağa kaydırılıp son değerimizle Xor’lanıyor. E tabii bu kadar işkenceden geçen sayının rastgele görünmemesi pek olası olmazdı. Aynı şekilde işlemler de bitwise yapıldığı için aslında oldukça hızlı bir algoritma. Tabii bunu bu şekilde bir cümlede anlatınca kafada pek bir şey oluşmuyor, o nedenle ben bunun Chrome’un da önemli bir kısmını oluşturan V8 motorunun kaynak kodunda yer alan implementasyonunun resmini koyayım.

Şimdi daha farklı yöntemleri inceleyelim. Unix benzeri işletim sistemlerinde, dolayısıyla GNU/Linux dağıtımlarında da yer alan sözde cihazlar vardır. İşletim sisteminin kök (/) dizininde yer alan /dev dizini altında sisteme normal şartlar altında fiziksel olarak bağlı cihazların temsili halleri birer dosya formatında bulunurken bahsettiğim sözde cihazlar da onlarla beraber bu dizinde bulunur. Bunlar /dev/random, /dev/zero, /dev/urandom, /dev/full, /dev/null gibi özel dosyalardır. Bizim odaklanacağımız sözde cihaz ise /dev/random olacak.

/dev/random cihazından veri okuyacak olursanız size bir akış olarak sürekli bir şekilde rastgele byte’lar üretecektir. Örneğin cat /dev/random gibi bir komutla bunları ham olarak okuduğunuzda işletim sistemi karakter tablosundaki birer karakterle eşleştirmeye çalışacağından anlamsız karakterler olarak gözlemleyeceksiniz.

Gelelim esas önemli kısma. /dev/random cihazının bizim için önemi şu: kendisi bu rastgele değerleri donanımlardaki çevresel gürültülerden elde ediyor. Aslına bakarsanız aritmetiksel yöntemlerden daha kullanışlı. Tabii kendi cihazınızın oluşturacağı elektromanyetik gürültüler hiçbir zaman tam olarak tahmin edilemez değildir. Bu nedenle /dev/random veya onun entropik olarak daha geniş bir havuza sahip olan kuzeni /dev/urandom “gerçek” rastgele sayı üreteci (True random number generator) kabul edilmiyor. Onlar da birer sözde rastgele sayı üreteci olarak geçmekte.

TRNG olarak anılan bazı çevresel donanımlar mevcut. Bunlar da çevresel bazı değerleri alıp işleyerek bunu yapıyor. Örneğin termal gürültü, fotoelektrik etki, ışın ayırıcı (beam splitter) etkisi veya diğer kuantumsal etkiler gibi, standart bir bilgisayar donanımında bulunmayan sensörlerle yapılan gözlemlerin sonucu ile amacına ulaşıyor. Bunlara hardware random number generator (HRNG) veya non-deterministic (deterministik olmayan) random bit generator (NRBG) de deniyor.

random.org gibi siteler ise atmosferdeki elektromanyetik gürültüyü kullanarak anlık olarak gerçek rastgele sayı üretme ve size bunu sayfa üzerinden ulaştırma vaadinde bulunuyor.

Son olarak kriptografik olarak güvenli olma konusuna gelelim. Gördüğünüz üzere sözde rastlantısal sayılar tahmin edilemez değil, sayıyı oluşturmadan önce onu tahmin edebilmek olası. Bu ise kullanımda büyük güvenlik açıkları doğuruyor. Örneğin yalnızca adresi bilen kişilerin ulaşabileceği bir sayfa veya dosya ismi belirlediniz ve bunu bir PRNG ile yaptınız. İşi bilen bir insan rastgele olduğunu düşündüğünüz o sonuca ulaşıp erişilmesini istemediğiniz o noktaya erişebilecektir. Senaryolar bundan ibaret de değil elbet, rastgelelik tahmin edilebilir olduğu zaman rastgelelik olmaktan çıkıyor. Bu gibi durumlar için cryptographically secure random number generator (kriptografik olarak güvenli rastgele sayı üreteci) adı verilen üreteçler kullanılır. /dev/random ve /dev/urandom sözde cihazları da kriptografik olarak güvenli olarak geçer. /dev/random, bir makine özelinde yaklaşık olarak tahmin edilebilir sonuçlar doğurabilir olsa da geniş bir perspektifte güvenli sayılabilir. Şayet özellikle kripto para, blockchain gibi güvenlik gerektiren bir platform kodluyorsanız bakmanız gereken rastgele sayı algoritmaları kriptografik olarak güvenli olanlar olmalıdır. Bunun için araştırma yapmalı ve uygun kütüphaneleri bulmalısınız. Geleceğe selamlar.